Loss Set ELT

A ELT Loss Set is a one of the options for doing any calculations involving Event Loss Tables using the Graphene system. Defining multiple ELT Loss Sets for analysis is supported (and common).

Structure

The general structure of an ELT Loss Set in Graphene is:

{
    "_schema": "LossSetELT_1.0",
    "paths": ["s3://example_bucket/uploads/ledgers/example_ledger_upload/losses.parquet",
              "s3://example_bucket/uploads/ledgers/example_ledger_upload/losses2.parquet"],
    "currency": "USD",
    "model": {
        "frequency": { "distribution_type": "POISSON" },
        "seasonality": { "min_time": 0, "max_time": 365.25 },
        "seed": false
    }
}

Another example:

{
    "_schema": "LossSetELT_1.0",
    "paths": ["s3://example_bucket/uploads/ledgers/example_ledger_upload/losses.parquet"],
    "currency": "USD",
    "model": {
        "frequency": { "distribution_type": "BINOMIAL", "index_of_dispersion": 0.5 },
        "seasonality": { "pairs": [ [1, 0], [31, 0.9], [100, 0.1] ], "subtype": "NON_CUMULATIVE", "interpolation": false },
        "seed": true
    }
}

Parameters

The parameters are defined as follows:

Parameter Name	Required	Type	Description
paths	Yes	array	Array of the unescaped S3 key prefix or full S3 key that represents a complete ELT loss data set. This path must be absolute.
currency	No	string	The currency in which the input currency values are defined. Defaults to the base currency if not set.
model	Yes	object	The model associated with the ELT data. Object is complex, so more details can be found below.

Note

Avoid S3 keys containing special characters as described in the S3 User Guide with the exception of delimiting / characters.

Model Parameters:

Parameter Name	Required	Type	Description
seasonality	Yes	object	Seasonality definition for the model. Object is complex, so more details can be found below.
frequency	No	object	Frequency definition for the model. Object is complex, so more details can be found below.
seed	No	boolean	If a seed value should be calculated and applied to the model. This will ensure values are the same for multiple runs. Default is true.

Seasonality Parameters:

Parameter Name	Required	Type	Description
pairs	No	array	Array of tuples in the form (Time, Probability). When supplied, implies Empirical seasonality type. If not provided, then seasonality type is Uniform.
subtype	No	string	Used in combination with pairs. Type of probability values in pairs. CUMULATIVE or NON_CUMULATIVE (default).
interpolation	No	boolean	Used in combination with pairs. If true, sampling will use linear interpolation between the provided time values. Default is false.
min_time	No	number	First day of simulated events. Is only required if pairs are not defined.
max_time	No	number	Last day of simulated events. Is only required if pairs are not defined.

Note

If you are using Decimal timestamps with 365.25-value handling for leap years and a Uniform seasonality distribution, and want a full year in the simulation, then min_time should be 0 and max_time should be set to 365.25. When using Posix please refer to the Timestamps documentation for Ledgers. Either pairs or min_time and max_time parameters MUST be provided.

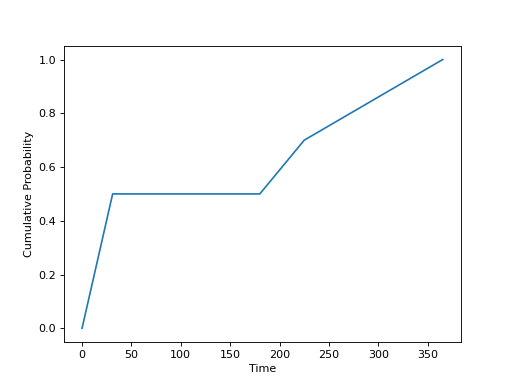
Sets of pairs in pairs describe the distribution of sampled time values over a defined range. interpolation impacts how sampled time values are distributed over the defined ranges in pairs. For pairs \(p_{n}, p_{n+1}\) when interpolation is off the likelihood sampled time values will be \(T_{n}\) is \(P_{n}\) and the likelihood they will be \(T_{n+1}\) is \(P_{n+1}\). When interpolation is on the likelihood sampled time values will be \(T_{n}\) is \(P_{n}\) and the likelihood they will be uniformly distributed over \((T_{n}, T_{n+1}]\) is \(P_{n+1}\).

The distribution for seasonality should be continuous. To ensure the distribution is continuous the first pair in pairs must have a probability of 0 and time values cannot be repeated.

subtype determines how probabilities are represented in pairs. When the subtype is CUMULATIVE a pair’s probability describes the likelihood that the sampled time value will be equal or less than the pair’s time value. The probabilities in pairs for CUMULATIVE must be non-decreasing and the last probability must be equal to 1. When the subtype is NON_CUMULATIVE a pair’s probability describes the likelihood that a sampled time value will be the pair’s time value. The probabilities in pairs for NON_CUMULATIVE sum must equal 1.

Note

pairs will be sorted by ascending Time value.

Example 1:

"seasonality": { "pairs": [ [0, 0.0], [1, 0.1], [31, 0.9] ] }

Sampled time values will have a 10% chance of being 1, and a 90% chance of being 31. If interpolation was set to true, then there would be a 10% chance of (0, 1], and 90% chance of a value sampled from a uniform distribution in the range (1, 31].

Example 2-A:

"seasonality": {
    "pairs": [
        [0, 0],
        [31, 0.5],
        [180, 0.0],
        [225, 0.2],
        [365.25, 0.3]
    ],
    "interpolation": false
}

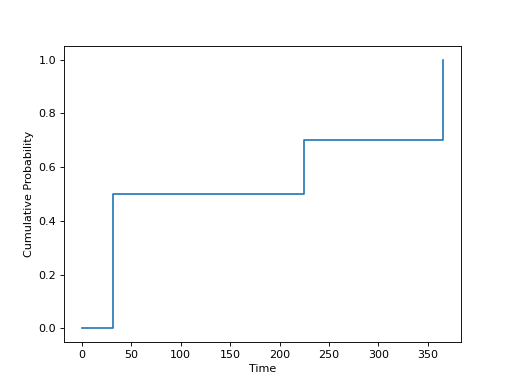
Example 2-B:

The same as 2-A, but with interpolation.

"seasonality": {
    "pairs": [
        [0, 0.0],
        [31, 0.5],
        [180, 0.0],
        [225, 0.2],
        [365.25, 0.3]
    ],
    "interpolation": true
}

Frequency Parameters:

Parameter Name	Required	Type	Description
distribution_type	No	string	Can be either POISSON, BINOMIAL or NEGATIVE_BINOMIAL. Default is POISSON.
index_of_dispersion	No	number	Variances/mean. Required for value for BINOMIAL or NEGATIVE_BINOMIAL calculations. Must be < 1 for BINOMIAL and > 1 for NEGATIVE_BINOMIAL distributions.

Note

FindNode Behaviour

It is important to understand that if you create an ELT template using some of the default values, they will not be populated until analysis time. Thus, if you want to search for a node using findnode, you must ensure that you add a search for an empty value.

For example, if you want to search for a model with a frequency distribution type of ‘POISSON’, you should structure the query as follows:

!? model.frequency.distribution_type | model.frequency.distribution_type == "POISSON"

Event Loss Table Data Storage

See ELT Format for the ELT input requirements.

Frequency Distribution Specification

For ELTs we offer the ability to partially parameterize the Poisson, Binomial and Negative Binomial distributions by providing an index of dispersion for the latter two. The index of dispersion is the ratio of variance to mean and allows us to exploit the additive properties of these three distribution types. More specifically:

\[\begin{split}& Poisson\\ & X_{i} \sim Pois(\mu_{x}) \\ & Y_{i} \sim Pois(\mu_{y}) \\ & X_{i} + Y_{i} \sim Pois(\mu_{y})\\ & \\ & Binomial\\ & X_{i} \sim B(n,p)\quad where\ \mu = np\\ & Y_{i} \sim B(m,p)\quad where\ \mu = mp\\ & X_{i} + Y_{i} \sim B(n+m,p)\quad where\ \mu = (m+n)p\\ & \\ & NegativeBinomial\\ & X_{i} \sim NB(n,p)\quad where\ \mu = \frac{n(1-p)}{p}\\ & Y_{i} \sim B(m,p)\quad where\ \mu = \frac{m(1-p)}{p}\\ & X_{i} + Y_{i} \sim NB(n+m,p)\ where\ \mu = \frac{(m+n)(1-p)}{p}\end{split}\]

When related to ELTs and models, the mean of the frequency distribution \(\mu\) is the sum of the rates in an event set. Thus, the mean is known based on the rates extracted from the ELT data that is attached to a model. For the negative binomial and binomial models the additivity of the events sets (and thus allowing us to incrementally build event sets from ELTs) depends on assuming a consistent index of dispersion. Given those, we can compute the negative binomial and binomial parameters.

\[\begin{split}& Binomial\\ & \mu = \sum (rates\ in\ eventset)\\ & D = provided\ index\ of\ dispersion\\ & p = 1-D\\ & n = \frac{\mu}{1-D}\\ & \\ & NegativeBinomial\\ & \mu = \sum (rates\ in\ eventset)\\ & D = provided\ index\ of\ dispersion\\ & p = \frac{1}{D}\\ & n = \frac{\mu}{D-1}\end{split}\]

Multiple ELT Data files in a Model

If you create a network with ELT template as input, you need to decide upfront if changes in the ELT template node will affect this network. If you decide that updating properties on the template node in the future, such as paths, is going to affect your calculation on this network, then you can add this template node without fixing the revision number. Using a fixed revision number will make the analysis results consistant even if you update the template node later.

To be able to build simulations incrementally a model can hold onto multiple event data sets. This is the ‘paths’ parameter in the template. Order of data files in the paths parameter matters, if the latest files contain definitions of events with the same IDs as the previous files, they will be ignored. This will generate a warning from the system.

When you add a new Event Loss Table (ELT) data to an existing model, the system goes through a process that involves difference calculation and identifying unique events. Here’s a detailed explanation of how this process occurs:

• When you add a new Event Loss Table (ELT) to an existing paths property, the system performs a difference calculation and identifies unique events within the new ELT based on event_ids

• The system compares the events in the new ELT with the events already present in the previous file.

• New events that have the same id as “existing” ones and are not duplicated. (they will be ignored, as stated above, and a warning will trigger)

• Events from the new ELT that do not match any existing events are tagged as “new” and a new event set is created for the model.

Note

S3 Path

Information on Relative S3 Paths format and special characters can be found in the Loss Set documentation.